Modular approach in scientific programming- Part I (Use of Single Language)

Introduction 

Most of the problems that we come across in scientific programming requires several lines of programs to be written. In addition to the type of problem under consideration, the exact number coding lines depends on overall methodology adapted for solution of problem. A typical finite element problem when modeled using C/C++ can contain even several hundreds of lines in the case of realistic post processing of results is to be achieved.

The inevitable redundancy of code in a such vast programs can be reduced to certain extent using certain programming techniques. The two most common and widely use techniques are given below.

1. In case of procedural languages like C, these techniques include smart use of functions, pointers, creation of custom header files etc.

2. Use of function /operator overloading, multiple inheritance are highly effective if the OOP ecosystem is deployed for developing such huge programs.

Despite of being effective to reduce the program length, these techniques are not enough. Fortunately, modern programming languages like Julia/ Python/R and others rely on use of dedicated packages built for specific task(s). E.g. to handle vast data contained in csv files, python uses 'pandas' package.

For numerical and scientific analysis, python features 'NumPy' and 'SciPy' packages. These packages contain several pre-compiled libraries which provide meaningful references to various useful functions and methods. E.g. in Julia, one can use following code to find determinant of matrix A given by

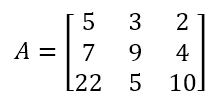
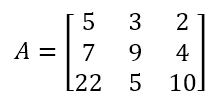
using LinearAlgebra

A= [5 3 2;7 9 4;22 5 10]

B=LinearAlgebra.det_bareiss(A)

show(B)

in order to write a traditional C style program for finding determinant of matrix, we need to code any of well-established numerical methods like ‘Doolittle decomposition’. However, it involves writing larger programs (which are susceptible to more errors) and (hence) requires precise debugging exercises before code is deployed.

Common Example of Interpolation

Let’s consider an example of finding the value of sine of angle as depicted below.

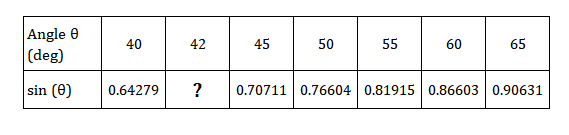
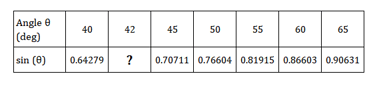
Clearly, the problem is of interpolation. We will use two languages C and Julia to find the solution for this problem.

Use of C language

First, we will use C program to model Newton Forward difference interpolation technique. In this C program, we have created custom header file “NCR.h” and placed it in same directory where our main program is located. The source file along with custom header file for this program can be downloaded from here

/*Interpolation using Newton's Forward Difference Method*/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include"NCR.h"/* Header file containing factorial and combination functions /
float sum=0;
int main(void)
{
int i,p,n;
float xp,u,val=0.0; / xp is value of x at which function is to be evaluated*/
printf("Enter the number of points for interpolation ");
scanf("%d",&p);
fflush(stdin);
float x,y,*A;
x=(float )malloc(psizeof(float));/* Values of x coordinates*/
y=(float )malloc(psizeof(float));/*values of Y coordinates /
A=(float )malloc(p*sizeof(float)); /* used to store differences /
//printf("--%d-- ",sizeof(x)/sizeof(float));
printf("Enter the angle values \n");
for(i=0;i<=p-1;i++)
{
scanf("%f",x+i);
}
fflush(stdin);
printf("Enter the sine values of angle\n");
for(i=0;i<=p-1;i++)
{
scanf("%f",y+i);
}
fflush(stdin);
for(n=0;n<=p-1;n++) / n varies from 0 to p-1*/
{
A[n]=0.0;
for(i=0;i<=n;i++)
{
A[n]=A[n]+(pow(-1,i)*y[n-i]*combination(n,i));
}
}
/* Computations for polynimial starts here /
printf("Enter the value of angle to be interpolated\n");
scanf("%f",&xp);
fflush(stdin);
u=(xp-x[0])/(x[1]-x[0]); / find value of u*/
for(i=0;i<=p-1;i++)
{
val=val+(A[i]*term(i,u)/fact(i)); /*Value of a required polynomial*/
}
printf("\nUsing Newton's Forward Difference Method,\n");
printf("The required value of sine at %.1f is %.8f\n",xp,val);
/* Computations for polynomial ends here */
getchar();
return 0;
}

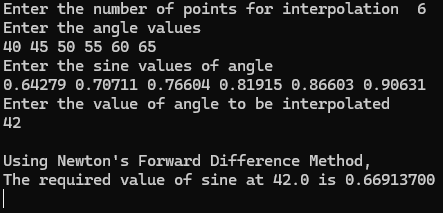
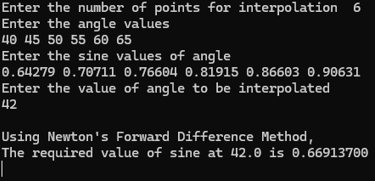
Output of C program

Use of Julia

In Julia, we have used a package named DataInterpolations.jl and all complicated calculations are done by LagrangeInterpolation () function as can be seen from program.

The source file for this program can be downloaded from here

using DataInterpolations

using Printf

# Data point definition

println("Enter the number of datapoints")

N=readline()

N=parse(Int,N)

x_set = []

y_set = []

println("Enter the angle values")

for i in 1:N

X=readline()

X=parse(Float64,X)

push!(x_set,X)

end

println("Enter the sine values for angle")

for i in 1:N

Y=readline()

Y=parse(Float64,Y)

push!(y_set,Y)

end

interp = LagrangeInterpolation(y_set, x_set)

# Interpolate at a given point

println("Enter the angle at which interpolation is to be carried out")

X_val=readline()

X_val=parse(Float64,X_val)

y_interpolated= interp(X_val)

println("The interpolated value of $X_val is ")

@printf("%.6f",y_interpolated)

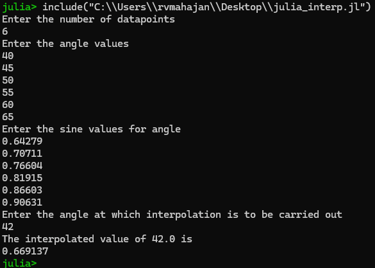
Output of Julia program

An interesting fact here is that, the package DataInterpolations.jl contains all the necessary code,libraries and references needed for calculating an interpolation value which is obtained via LagrangeInterpolation () function. Note that, it is a predefined function available with this package. Thus, the actual code involved in calculation of interpolation value remains hidden from user.

This can be thought of writing some code in background and calling it in real-time without worrying about its composition.

Problem statement affects Choice

If you ask me about what option I prefer out of C and Julia, I will prefer C language if the scope of problem is limited to finding interpolated value only. This is for the reason of flexibility that C language definitely offers for code customization.

Julia can be preferred when problem of finding an interpolated value is sub task of a larger problem. i.e. if solution of this problem is an input to another problem.

Leave a reply