Machine epsilon in scientific computing

Machine epsilon in scientific computing

Like every other man-made machine, existing computers also have some limitations. These limitations are with respect to:

• Data storage capacity

• Data storage and retrieval speed

• Data processing speed

• Minimum and maximum numbers which computers can identify

The magnitudes of these limitations vary from computer to computer. Undoubtedly, from a computational point of view, all of these are important. Yet, minimum and maximum numbers which computers can identify significantly affect the implementation of computer-oriented numerical/scientific programming. With this perspective, this article explains the concept of machine epsilon in scientific programming.

Consider the following calculations performed on a Julia REPL terminal.

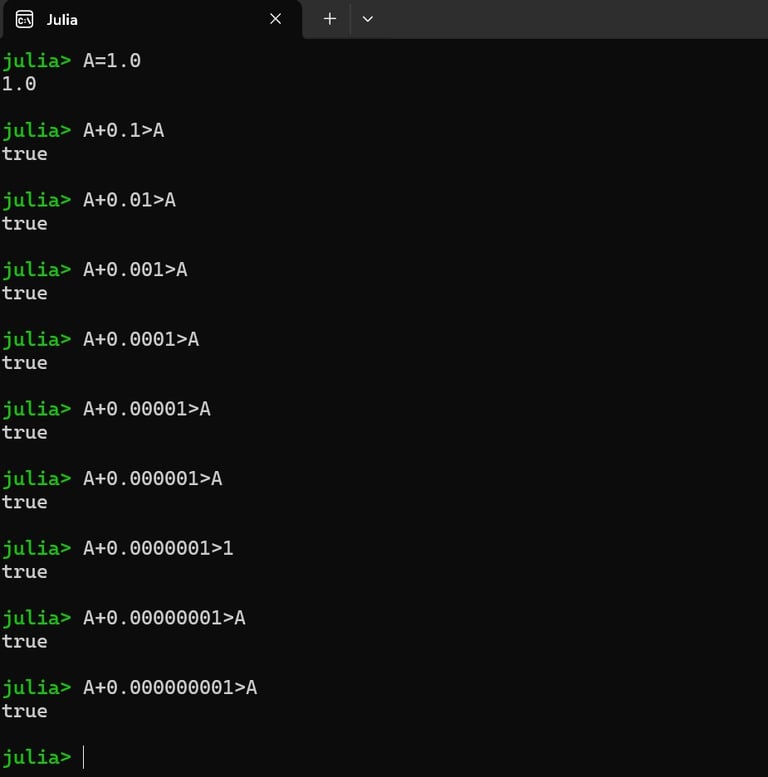
It is observed that the variable A has an assigned value of 1.0, and if we successively go on adding smaller and smaller numbers to A, as seen in the figure above, we will notice that the result of addition is greater than 1.0. This basically happens because the computer is in a position to identify all of these small numbers that we added to A = 1.0. But the question is:
What is the smallest number which a computer can identify?

Again, consider the following calculations performed on a Julia REPL terminal.

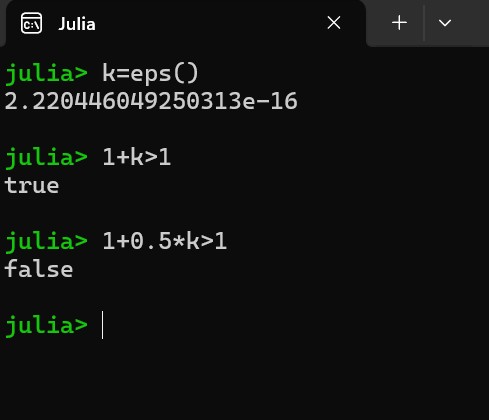
Here we use the eps() function to retrieve a very small number and assign it to the variable k. Further, if we add this number to 1.0, the result of addition is again greater than 1.0. But if we add any number which is less than k, say 0.5k, to 1.0, then the result of this addition is not understood by the computer and hence we notice that the Julia REPL terminal gives a false result for the comparison 1 + 0.5*k > 1.

This happens because of the fact that the minimum value that our system could understand here was k. And as seen from the figure, its value is 2.220446049250313e-16. This is the minimum distance between two floating-point values a computer can identify. Any value which is greater than or equal to this distance is identified by the computer. However, if the distance between two floating-point values is less than this interval, then it cannot be identified by the computer. (By the term "distance," we mean numerical difference here.)

This value is called ‘Machine Epsilon,’ which is usually denoted by the symbol ϵ. It is interesting to note that the machine epsilon depends on the word length of the processor  i.e., whether you are working on a 16-bit, 32-bit, or 64-bit machine.

In our next article, we cover convergence of numerical solution.

Leave a reply